Compressed Sensing For Classification

Introduction

Compression is ubiquitous and powerful. We apply it to reduce images of megapixels to a few percent the size, and we cannot see the difference. But why bother collecting all those data in the first place? This is where compressed sensing comes into play. It is useful when the data acquisition is expensive or too long. For example, compressed sensing allows us to reduce the time patients spent in MRI machine to about 1/5th as before.

It is not hard to imagine that if we were to do classification, the amount of data needed is much less! This is illurstrated by this Picasso’s painting: we can still recognise the bull with just a few lines! In this first blog, I would like to introduce the idea with the algorithm by B. W. Brunton et al. (2016). The outcome is that a few sensors could achieve a highly accurate classification when we need more sensors to represent the object. Picasso Bull minimalism The algorithm is Sparse Sensor Placement Optimization for Classification (SSPOC) algorithm. The paper comes with a great video abstract and the code used is in matlab. P.S. Huge fan of the work done by this group of academics, especially Prof. Steve Brunton. Check out his work at: eigensteve.com! Amazing researches at Kutz group too!

This algorithm is very useful when the sensor is expensive, such as the sensors in the ocean to study weather and climate, the questions in a market research questionaire etc. The authors have demonstrated dog/cat image classification and human face image classification.

I will first give a very simple picture of the algorithm then in more rigorous terms (I mean, all the maths). At the end, some ideas and applications will be discussed.

Algorithm in pictures

We will demonstrate the algorithm on the cat/dog classification problem using images of 121 cats and 121 dogs. The images are 64-by-64, i.e., 4096 pixels. To put the goal in simplier terms, we want to classify a potential picture accurately measuring as few pixels as possible. The original data is

Feature extraction

4096 pixels is a lot of information and let us first reduce the dimension. The most common approach is principle component analysis (PCA) or singular value decomposition (SVD). Here are the first four modes: 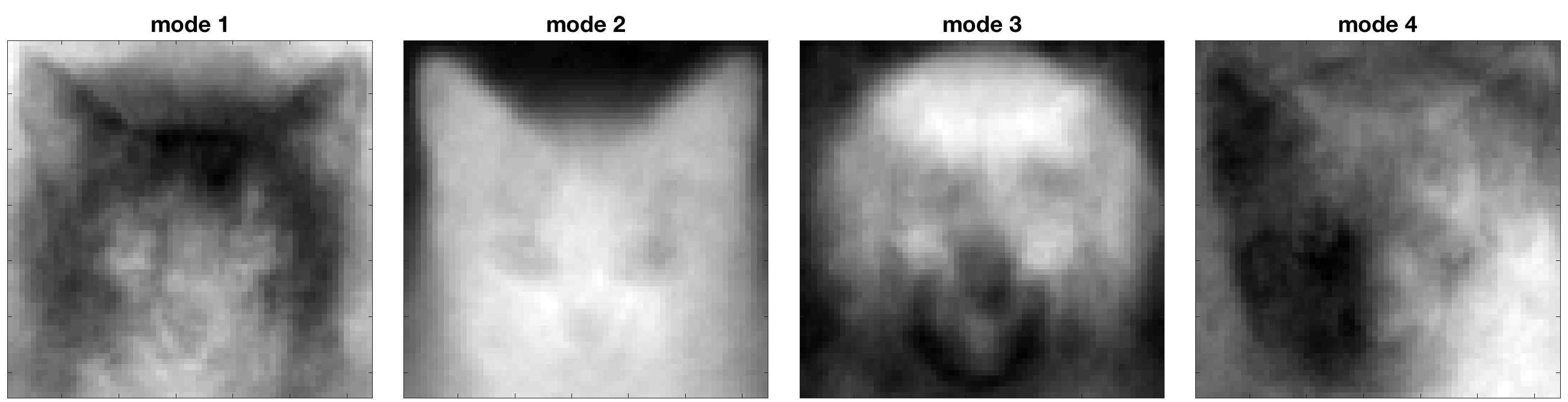The modes are ‘features’ and they come out in descending order of ‘importance’. The first one is a mean face. Mode 2 captures the general face shape of a cat, especially the pointy ears. Mode 3 has representative dog features. If we look at the singular value spectrum, we see that the dog/cat face data set lives on a relatively low dimension. So we then use a linear classifier on the rank truncated data.

Linear classifier

The full rank is 242 and rank 5 means we use the first 5 modes to represent the data (i.e. ~2%). In the linear discriminant analysis (LDA), the data is projected on to 1D line and the distribution of the data along the line is represented by the following histogram. The blue and red lines are the centroids of the two classes

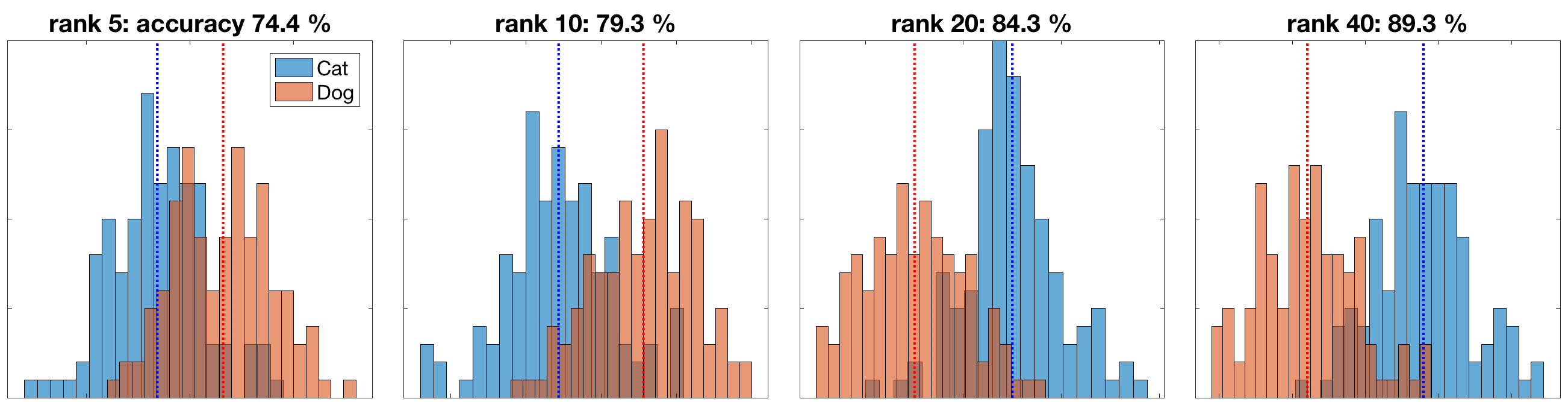
If a data point is closer to the blue line, it is classified as a cat; otherwise, a dog. So such a simple model can achieve quite high accuracy. Pretty cool.

Sparse sensor location

Under the LDA framework, the paper constructs an $\mathrm{\ell}_1$ -minimisation problem to select the least number of sensors given a certain rank truncation. The example for rank 20 results in 20 sensors. The locations of the sensors are in red. If we train a new LDA classifier on the sparse sampled data, we can get a 83% accuracy! It is fascinating how few data we need. Think of it as a computer playing jigsaw puzzle. With only 20 pieces out of 4096, it does a good job guessing whether the puzzle is a dog or cat. Obvisouly, the trick is which 20 pieces to choose. If we look at the sensor locations, they are mostly at the face region. One is at the top, probably identifying the pointy ear. Several are around the eyes and mouth.

Algorithm in equations

Ok, time for some maths! Here is the notations

Fully sampled original signal $\vec{x} \in \mathbb{R}^n$ . I will drop the vector notation and use $x$ instead of $\vec{x}$
Full data matrix with $m$ samples: $X = [x_1, x_2, ..., x_m]\in \mathbb{R}^{n \times m}$
Sparse basis (from the signal space to the feature space): $\Psi$
Sampling matrix: $\tilde{\Phi} \in \mathbb{R}^{p\times n}$
Subsampled signal: $\tilde{x} = \tilde{\Phi} \vec{x}$ , where $\tilde{x} \in \mathbb{R}^p$

principle component analysis(PCA)

PCA/SVD is commonly used for dimension reduction/feature extraction. Have a look at this quora post to get an intuition. SVD gives

$X = \Psi \Sigma V^*$

Take the first $r$ largest singular value and the corresponding eigenvectors $\Psi_r$ . The eigenvectors form a basis to project the data from the full measurement space into the reduced $r$ -dimensional PCA space (also known as feature space):

$\Psi_r^T: \mathbb{R}^n \rightarrow \mathbb{R}^r, x \rightarrow \vec{a}$

linear discriminant analysis(LDA)

In the authors words: “LDA attempts to find a set of directions in feature space $\vec{w} \in \mathbb{R}^{r\times (c-1)}$ (discrimination vectors), where the between-class variance is maximized and the within-class variance is minimized’’. After projecting along this direction, the data points of the same class are clustered together (small in-class variance) while they are separated from other classes (large between-class variance) A good picture is this one here.

LDA_intuition

The discrimination vectors projects maps $\vec{a}$ in the feature space to the decision space $\eta$ where

$\eta = \vec{w}^T \vec{x} = \vec{w}^T\Psi_r^T x$

SSPOC

This is the core part, where we select where to place the sensors. The paper states the optimisation goal being “to recompute a new projection to decision space directly from the data matrix composed of sparse measurements”. Thus wer are looking for a sparse vector $\vec{s}$ so that $\eta = \vec{s}^T x$ i.e., $\vec{s} = \Psi_r \vec{w}$ To promote sparsity means that we would like as many of the entries of $\vec{s}$ to be zero. It is often solved via the approximate $\mathrm{\ell}_1$ minimisation:

$\vec{s} = \underset{\vec{s'}}{\mathrm{argmin}} \lVert\vec{s'}\rVert_1 , \text{ subject to } \Psi^T_r \vec{s'} = \vec{w}$

It has been solved using the cvx, a convex optimisation solver.

Classify compressed sensing data

Given the $q$ nonzero elements of $\vec{s}$ , we can construct a sparse sensing matrix $\hat{\Phi} \in \mathbb{R}^{q\times n}$ .
The sparsely measured data is $\hat{X} = \hat{\Phi} X$ .
We will learn a new discrimination vector and use the new centroids to classify new examples.

In the end, let me show the contrast between the fully sampled and data using SSPOC, that gives us 83% accuracy. Each stripe corresponds to 20 pixels given the optimal sparse sensing pattern.

Final thoughts

Some ideas I would like to explore about the algorithm:

How large a sample does SSPOC need?
how robust the algorithm is? Does it generalise to similar unknown samples well?
Is there any metric to justify the sensor location? e.g., some information criteria?
During the $\mathrm{\ell}_1$ optimisation, the vector $\vec{s}$ is not uniform so should we use the weights to fine-tune our sprase ‘sampling’?

Recently, this group have explored how to use as few sensors to reconstruct the original signal (Data-Driven Sparse Sensor Placement for Reconstruction, Manohar K. et al, 2017). The reconstruction task is more akin to the most well-known compressed sensing use case while the classification bears an interesting twist. I feel strongly that a joint algorithm with nonlinear classifier could make it more powerful or robust. The hierarchical classification mentioned by Prof. Bing Brunton is also very desirable. I imagine that there could be a cascade of classifiers, which become more and more expensive and accurate. Maybe it can be used in a production line to reject faulty parts.

This is the first time writing tech blogs and I would like to introduce the idea in a more intuitive way. Please let me know any comment! I hope I have cited everything and please suggest any missing link. Thank you for reading.